子集枚举(SOS)

code

//iterative version
for(int mask = 0; mask < (1<<N); ++mask) {
	dp[mask][-1] = A[mask];	
    //handle base case separately (leaf states)
	for(int i = 0;i < N; ++i){
		if(mask & (1<<i))
			dp[mask][i] = dp[mask][i-1] + dp[mask^(1<<i)][i-1];
		else
			dp[mask][i] = dp[mask][i-1];
	}
	F[mask] = dp[mask][N-1];
}

//memory optimized, super easy to code.
for(int i = 0; i<(1<<N); ++i)
	F[i] = A[i];
for(int i = 0;i < N; ++i) {
    for(int mask = 0; mask < (1<<N); ++mask){
        if(mask & (1<<i))
            F[mask] += F[mask^(1<<i)];
    }
}

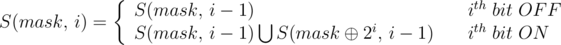
S(mask,i) 表示第0位到第i位不同的子集

时间复杂度$O(N2^N)$

tutorial

https://codeforces.com/blog/entry/45223
https://blog.csdn.net/weixin_38686780/article/details/100109753

例题

• Special Pairs

• https://blog.csdn.net/tianyizhicheng/article/details/100392870
  https://blog.csdn.net/noone0/article/details/78290029

• Compatible Numbers

• Vowels

• Covering Sets

• COCI 2011/2012 Problem KOSARE

• Vim War

• Jzzhu and Numbers

• Subset

• Jersey Number

• Beautiful Sandwich

• Pepsi Cola(resembles above discussion problem). Need to join this group.

• Uchiha and Two Products(resembles above discussion problem)

• Strange Functions(Same as above discussion problem)

• Varying Kibibits
  EDIT: Practice problems are now arranged in almost increasing order of difficulty.